为什么逢赌必输?看完这个后就知道了
以周润发的《赌神》和周星驰的《赌圣》为代表的赌片曾经风靡一时,影片中的人物更是成为大家争相模仿的对象。

《赌神》高进,周润发饰

《赌圣》周星星,周星驰饰
赌桌之上,他西装革履,踌躇满志、处变不惊,在最后一刻逆风翻盘,赢得赌局。这样的人设放在什么时候都是让人啧啧称奇的,就更不用提周润发、周星驰本身对角色的加持了。

有时影视剧看多了,人就容易分不清真假。
看完了赌神们在赌场中神乎其神的操作,有些人也就认为自己也能像他们一样,在赌桌上呼风唤雨,一夜暴富不是梦。

于是,急匆匆地就准备去赌桌上大显身手,坐实他xx地区赌神的称号。
然而,赌博,是充满陷阱与算计的游戏。你以为你是赌神,最终能够飞黄腾达,而实际上你只是任人宰割的赌徒,最终只有家破人亡的结局。

近年来公安机关严打“黄赌毒”,于是一些不法之徒便将赌桌搬到了线上,通过各种渠道散发涉赌违法信息,大肆招揽参赌、收取赌资。
总有那么些人觉得自己的赌技堪比赌神高进,想趁机大捞一把,于是兴冲冲地上了贼船着了道。
你以为在赌桌上靠的是算计和运气,而事实上赌桌之上的输赢全是被暗箱操控好的。作为玩家,纵使赌神在世,也是斗不过游戏背后的程序的。

于是,我们经常看到揭露赌博骗局的新闻报道——

其实,赌博游戏是被暗箱操作的,赌博网站可以通过程序控制输赢结果和输赢比例。
例如当天配了10%,在保证总盈利在10%的基础上,针对个人,网站甚至可以控制单场数字的结果,从而保证庄家一本万利。
也就是说,你以为你赢了是你的本事,而事实上这也只是庄家设计好的圈套而已。

此外,类似的鬼把戏还有特制眼镜加“魔术牌”,可以从背面看出牌面的点数。

还有外形酷似手机的便于出老千的电子换牌器,总之只有你想不到没有做不到的。

或许有人在想,这种容易出老千的赌局我肯定不会碰的,但是那种纯碰运气的游戏比如投硬币,我还是有机会赢的吧?
对不起,即使是完全公平、没有一点猫腻的赌局,作为下注的赌徒,你也没有任何赢面的。
为什么?
因为你靠的是运气,而赌博背后是狄利克雷、伯努利、高斯、纳什、凯利这样的数学大师。
看完以下内容,你应该就能懂得逢赌必输的道理了。
掷硬币:50%概率背后的陷阱
我们先来看一个最简单的玩法:抛硬币。
规则是这样的,正面赢反面输,如果赢了可以拿走比赌注多一倍的钱,如果输了则会赔掉本金。

这个游戏是不是简单又公平?
有一个人叫苏苏,他拿出100元来玩这个游戏,每次下注5元,这样苏苏就至少有20次的下注机会。
但是,苏苏运气不太好,第一把就是反面,输了5块钱。
要继续吗?
苏苏觉得没什么,才输了五块钱而已,而且不管怎么说,赢面都有50%,下一把就可以赢回来。
结果,苏苏很快就输光了所有钱。
苏苏百思不得其解,明明是很公平的50%赢面,按道理在50%概率下他至少不会亏本,可为什么最后会输光呢?
苏苏自以为看到了50%的概率,看懂了游戏背后的逻辑,然而,他看到了概率却没有看到背后的陷阱。
大数定律:屡被误解而成陷阱
大数定律是什么?
数学家伯努利提出,
假设n是N次独立重复试验中事件A发生的次数,p是每一次试验中A发生的概率,那么,当N趋于无穷时:
式中,n表示发生次数,N表示试验总次数。
也就是说,大量重复的随机现象里其实藏着某种必然规律。
以掷硬币为例,当投掷次数足够大时,出现正(反)面的频率将逐渐接近于½,且随着投掷次数的增加,偏差会越来越小,如下图,这是最早发现的大数定律之一。
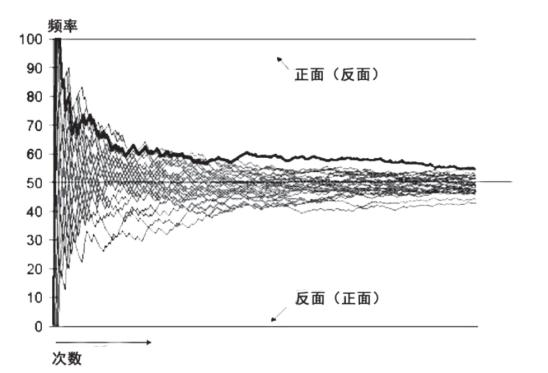
掷硬币频率分布图
苏苏觉得游戏是公平的——一正一反,均为50%概率。按照大数定律来说,这是必然规律。
然而,苏苏没想到正是这种他以为的“公平”,让他误解了大数定律,陷入了“赌徒谬论”里。

从表面概率看,这确实是场公平的游戏。
但这种公平是有条件的,而这就是一般人容易忽视的。
大数定律的条件是“大量重复的随机现象”,即只有足够多次试验才能使得硬币正反面出现次数与总次数之比几乎等于½。多少次才算“足够多”呢?没有人知道。因为,概率论给出的答案是——无穷大。
而相反的,投掷硬币次数越小,大数定律的身影就越模糊——可能10次中5正5反,也可能9正1反,也可能10正0反或0正10反……
因此,如果苏苏将此定律用于个人有限的对赌游戏中,现实往往是,在远未达到“足够多”次试验时,他就已经输光了。他有100元是这个结局,1000元也是如此,就算是1000万元也还是如此,因为苏苏永远不可能会有“足够多”的钱。

“输赢概率为50%”,这本身就具有很大的误导性。在硬币抛出之前,50%的概率代表的是可能性;在硬币抛出之后,50%代表的是结果的统计平均值,却并不是实际分布值。这是苏苏对大数定律的误解,也是一般人对于此定律的误解。
把“大数定律”当“小数定律”,觉得游戏是无条件“公平”的,正面和反面出现的频率都为½。这种在潜意识里被奉为圭臬的“公平”,紧接着让苏苏踏入了第二个误解——“赌徒谬论”。
赌徒谬论:下一把就能赢回来
大数定律有一个潜台词——当随机事件发生的次数足够多时,发生的频率便趋近于预期的概率。
然而,人们常常错误地理解为:随机意味着均匀。
如果过去一段时间内发生的事件不均匀,大家就会“人工”地从心理上把未来的事情“抹平”。也就是说,如果输了第一把,那么苏苏会认为下一把的赢面会更大,于是继续游戏,甚至下更大的赌注。
这种下一把就可以赢回来的强烈错觉,就是“赌徒谬论”。

当苏苏掷硬币连输后,他的心里会突然冒出一个想法——稳住,风水轮流转,下一把我很有可能“翻身农奴把歌唱”!
而事实上,高中概率论告诉我们,两次掷硬币的活动是独立事件,没有任何联系,不会相互产生影响。

因此,赌局是没有记忆和感情的,就算苏苏曾经输光了家底,它也不会在下一局中给他更多赢面。
北
套路
南
赌场下注:如何获得最大收益?
某一天,苏苏陪他的女朋友到澳门旅游,路过赌场,苏苏想起了之前掷硬币输掉的钱,他决定在这里把它们赢回来,于是他走进了赌场。
苏苏决定从哪里跌倒就从哪里站起来,他依然选择了这个1赔2(不包括本金)的简单赌局——扔硬币下注,假设赌注为1元,硬币如果为正面则净赢2元,如果为反面则输掉1元,每一次的押注都可投入任意金额。
苏苏这次的总资产依然是100元,有了上次的教训,苏苏决定先做一番思考再下注——
要不就干脆一点,all in!女朋友还在这看着呢,干脆一次性把100元全押上,运气好就能获得200元。运气不好的话……只能乖乖陪女朋友逛街了。
上次就吃了大意的亏,这次谨慎点,慢慢来。我每次只下注1元,这样输得少些。可是这样玩,别人一次性能赢20、200,我才赢2元,也很难受啊……
所以,到底该以多少比例下注才能获得最大收益呢?
苏苏陷入了沉思……
苏苏不知道,凯利公式早就将答案写在了某一本数学书里——
每次下注比例为当时总资金的25%,这样就能获得最大收益。
让我们先抬出凯利公式这尊大佛:
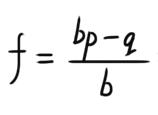
以下注释稍微有点令人头大,但受过物理、化学摧残的你一定可以的!
在公式中,各参数意义为:
f = 应投注的资本比例(苏苏想要得出的结论)
p = 获胜的概率(也就是抛硬币正面的概率);
q = 失败的概率,即(1 - p)(也就是硬币反面的概率);
b = 赔率=期望盈利 ÷可能亏损(也就是盈亏比);
公式上面的分子(bp-q)代表“赢面”,数学中叫“期望值”。
苏苏看到这个公式后连忙找笔计算:
硬币抛出正反面的概率都是50%,所以p、q获胜失败的概率都为0.5,而赔率=期望盈利÷可能亏损=2元盈利÷1元亏损,赔率就是2,要求的答案是f,也就是(bp - q) ÷ b = (2 * 50% - 50%) ÷ 2 = 25%。

于是,根据凯利公式的计算结果,苏苏每次应该拿出当前手中资金的25%来进行下注。
但是,一朝被蛇咬十年怕井绳的苏苏仍然不敢贸然行动,于是他找到学计算机的同学光光,让他帮忙模拟一下投注的收益情况。很快,光光就将两种模拟结果发给了苏苏。
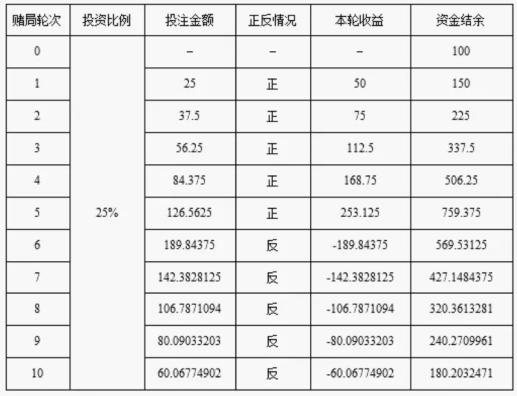
表1 25%投注下10次收益表
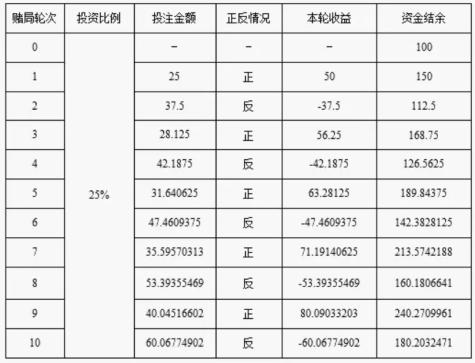
表2 25%投注下10次收益表
表1从先正后反的情况计算了收益,而表2则计算了正反分布交错情况下的收益结果。
比较两表,苏苏发现两种情况下收益是相等的,硬币出现正反面的先后顺序对于最终收益的计算结果并无影响。
按25%的投注比例进行投注,收益基本呈现稳步增长的大趋势。
苏苏如果按照之前假设的100%投注比进行投注,10次当中只要出现任意一次的反面,就会彻底输光身上的所有钱,直接出局,而且每轮反面概率还为50%。
而每次1元1元地投注,也就是投注比例为1%的时候,10次数学上的收益为100+10×50%×2+(-1)×10×50%=105,这风险很小,不过收益太低。
所以,凯利公式才是最大的赢家。
苏苏明白了,所有赌局都是一场数学游戏,哪怕是麻将扑克背后其实都是概率论的问题,而赌场操盘者每一次下注都会遵循数学原则。
凯利公式不是凭空设想出来的,这个数学模型已经在华尔街得到了验证,除了在赌场被奉为“胜利理论”,同时也被称为资金管理神器,它是比尔格罗斯等投资大师的心头之爱,巴菲特依靠这个公式也获取了很多收益。
但是凭你读书时上课打瞌睡、输了只知道倍投翻本的可怜知识,以及九九乘法表的那点算力,还是先老实读完以下三条准则。
(1) 期望值(bp-q) 为 0 时,赌局为公平游戏,这时不应下任何赌注。
(2) 期望值(bp-q)为负时,赌徒处于劣势,更不应下任何赌注。
(3) 期望值(bp-q)为正时,按照凯利公式投注,赚钱最快,风险最小。
最终结论只有一个:除非 100%,否则任何时候都别赌上全部身家,即使贏率相对较高也要谨慎。
有人可能说,我又不是与赌场对赌,我只要贏了对手就行了无论是你还是对方,贏者都是要给赌场“流水”的,赌的时间一长两者都是在给赌场打工。
现代赌场自己做庄的可能性很小,他们更依赖数学定理获取益。对于那些小型赌场和线上赌场,怎么就确定你的对手不是赌场本身呢?
没有谁能说服一个堕落的赌徒,因为这是人格的缺陷。如果你是一个具有理性精神的人,就别再迷恋所谓的运气。你怎么可能赢得了庄家?

论理性,没有人能比赌场老板更理性。论数学,没有人能比赌场老板请的专家更精通数学。论赌本,没有人能比赌场老板的本钱更多。
如果你想真正贏得这场赌局,法则只有不赌。